1. Appendix: Detailed web flyers
1.1. Winter/Spring 2026 - math for research extended flyer
Math for Research Working Group
First meeting: Monday, February 2, 2026
Meeting times/locations:
Goal: Math as it is used in research
Most research problems do not have solutions, so we use math to gain insight into these problems that do not have a solution.
This involves beautiful and intriguing techniques that break functions down into component parts. Two of these approaches are Taylor Series and Fourier Analysis – key parts of the reasercher’s toolbelt.
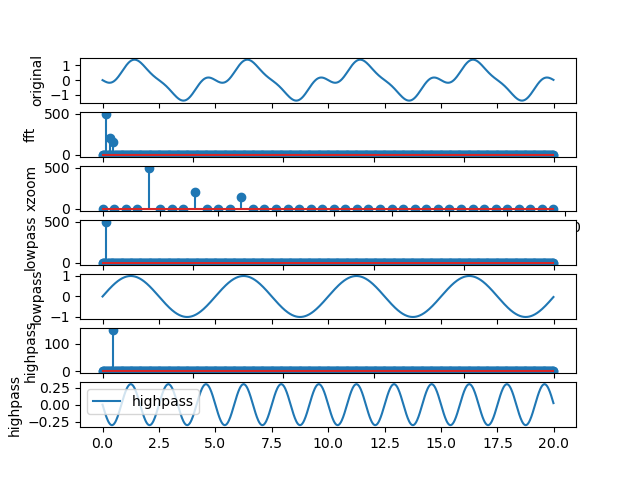
Figure 1.1.1 Filtering a sum of three sine waves.
This working group aims at motivated students who are about to enter the precalculus and calculus phase of their studies. It gives glimpes into how those subjects will be used.
We do not assume knowledge of calculus, and we introduce all the ideas we use beyond algebra.
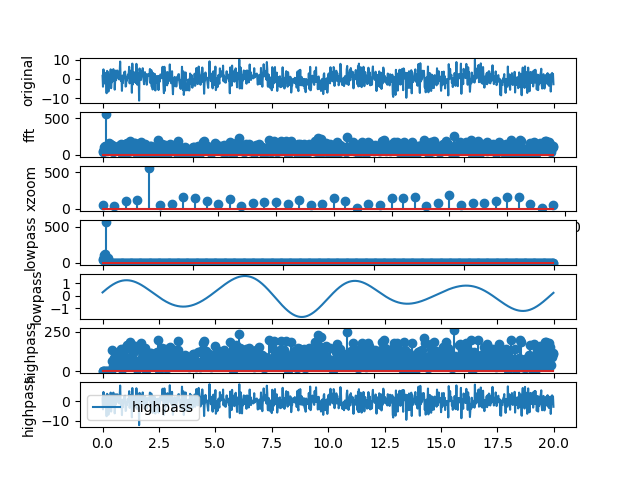
Figure 1.1.2 Filtering a noisy signal.
We meet in videoconference, and it is a no-anxiety working group: we do advanced material, but we take it easy and we make constant use of visual approaches.
We do not do any computer programming, but we use computers to make plots.
Students and faculty:
Please get the word out to students interested in research technique. We look forward to seeing you on February 2nd!
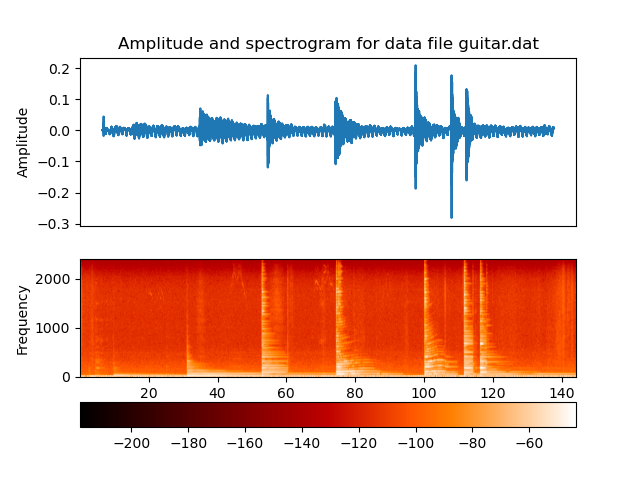
Figure 1.1.3 Spectrogram of notes and some bending on a guitar.
1.2. Fall/winter 2025 - visualizing algebra extended flyer
Visualizing Algebra Working Group
First informational meeting
Meeting times/locations:
Goal: building intuition for mathematics
Our goal in this working group is to build agility and wide experience in visualizing and solving equations. It is aimed at students taking the Algebra/Geometry sequence typical in high schools, though more experienced students will also find much of interest.
This is a crucial part of developing the intuition for mathematics that helps when you start using it in real research projects.
We start with a review of previous algebra aimed at understanding why we were given certain rules. Then we will spend most of our time understanding the structure and shape of functions.
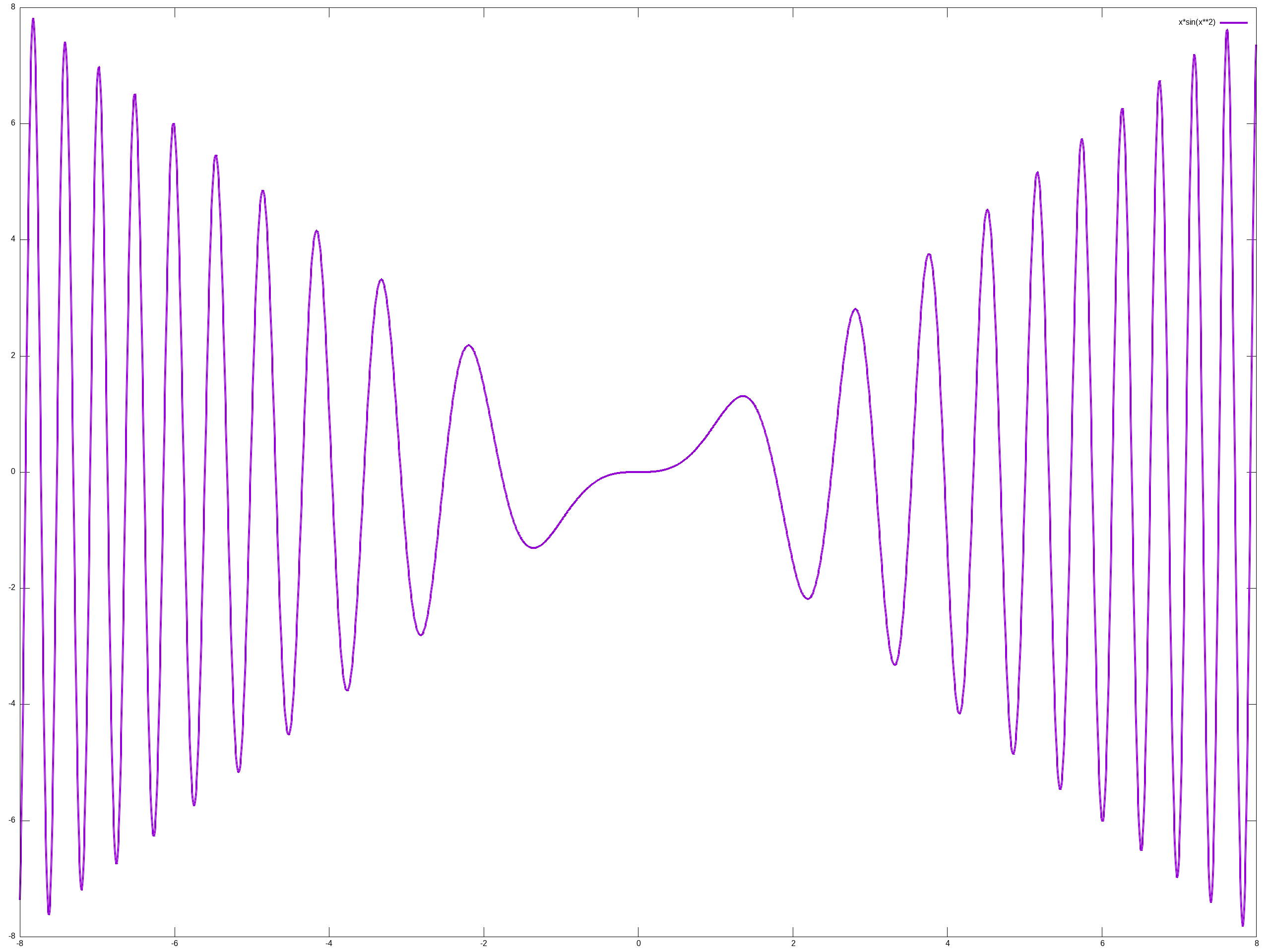
Figure 1.2.1 Plot of \(x \sin(x^2)\).
This will take us on a tour of the pantheon of functions to develop a feeling for their visual appearance and then their deep structure: polynomials, rational functions, algebraic functions, transcendental functions.
The tour of functions is visually and conceptually intriguing, touching upon how equations bring about reduction in the dimension of geometric figures by slicing them.
Other topics will include learning the symbolic algebra package sympy, which we will use to study systems of equations and factoring polynomials.

Figure 1.2.2 A plane slicing a curved surface generates a 1-dimensional curve.
No prerequisites – we do not assume knowledge of calculus, and we introduce all the algebra ideas we use – this is a fun, no-anxiety romp through math.
Please get the word out to students interested in research technique. We look forward to seeing you on October 6th!